Method of solar calculation in energyPRO

In energyPRO a solar collector producing heat and a photovoltaic producing electricity can be modelled. Setting up the units is based on time series with solar radiation and ambient temperature, information about location, orientation and performance (found in datasheets from the manufacturer).

Definitions

Symbol	Units	Description
\(\alpha\)	[ ° ]	Solar altitude angle (90o - z)
\(\phi\)	[ ° ]	Latitude
\(\delta\)	[ ° ]	Solar declination angle
\(\gamma\)	[ ° ]	Orientation of inclined plane, south = 0, west = 90
\(\gamma_t\)	[]	Temperature coefficient for photovoltaic module efficiency
\(\theta\)	[ ° ]	Angle of incidence of beam radiation on inclined plane
\(\theta_l\)	[ ° ]	Longitudinal angle of incidence of beam radiation on inclined plane
\(\theta_t\)	[ ° ]	Transversal angle of incidence of beam radiation on inclined plane
\(\omega\)	[ ° ]	Hour angle
\(\rho\)	[]	Reflection factor
\(\theta_z\)	[ ° ]	Solar zenith angle
\(\lambda_{misc}\)	[]	Losses from the photovoltaic-module to the grid
\(a\)	[]	Incidence angle modifier coefficient
\(A\)	[ \(m^2\) ]	Total solar collector area
\(A_I\)	[]	Anisotropy index
\(f\)	[]	Modulating factor
\(I\)	[ \(W/m^2\) ]	Total radiation on a horizontal plane
\(I_b\)	[ \(W/m^2\) ]	Beam radiation on a horizontal plane
\(I_d\)	[ \(W/m^2\) ]	Diffuse radiation on a horizontal plane
\(I_{diff}\)	[ \(W/m^2\) ]	Diffuse radiation on an inclined plane
\(I_{dir}\)	[ \(W/m^2\) ]	Beam radiation on an inclined plane
\(I_o\)	[ \(W/m^2\) ]	Extraterrestrial radiation on a horizontal plane
\(I_{ref}\)	[ \(W/m^2\) ]	Ground reflected radiation on an inclined plane
\(I_s\)	[ \(W/m^2\) ]	Total radiation on an inclined plane
\(I_{sc}\)	[ \(W/m^2\) ]	Solar constant, 1367 \(W/m^2\)
\(I_{bn}\)	[ \(W/m^2\) ]	Beam radiation at normal incidence
\(I_{on}\)	[ \(W/m^2\) ]	Extraterrestrial radiation at normal incidence
\(I_{STC}\)	[ \(W/m^2\) ]	Radiation at standard conditions (1000 \(W/m^2\)) (photovoltaic)
\(K_θ\)	[]	Incidence angle modifier
\(K_θ\)(\(\theta_l\))	[]	Longitudinal incidence angle modifier
\(K_θ\)(\(\theta_t\))	[]	Transversal incidence angle modifier
\(a_1\)	[W/( \(m^2\) °C)]	First-order coefficient in collector efficiency equation
\(a_2\)	[W/( \(m^2\) °\(C^2\))]	Second-order coefficient in collector efficiency equation
\(K_T\)	[]	Ratio of total radiation on a horizontal plane to Extraterrestrial radiation
\(n\)	[]	Day of year
\(n_0\)	[]	Intercept (maximum) of the collector efficiency
\(NOCT\)	[ °C ]	Nominal Operating Cell Temperature (photovoltaic)
\(P_{pv}\)	[ W ]	Electricity production from a Photovoltaic module
\(P_{max}\)	[ W ]	Installed capacity, photovoltaic
\(P_{elec}\)	[ W ]	Electricity production to the grid from the photovoltaic plant
\(R_b\)	[]	Ratio of beam radiation on an inclined plane to beam on horizontal
\(R_d\)	[]	Ratio of diffuse radiation on an inclined plane to diffuse on horizontal
\(R_r\)	[]	Ratio of reflected radiation on an inclined plane to total radiation on horizontal
\(s\)	[ ° ]	Inclination of surface
\(t_a\)	[ °C ]	Ambient temperature
\(t_m\)	[ °C ]	Solar collectors average temperature
\(T_{cell}\)	[ °C ]	Photovoltaic operation cell temperature
\(T_{STC}\)	[ °C ]	The cell temperature at standard conditions (25 °C) (photovoltaic)
\(T_{TST}\)	[ h ]	True Solar Time
\(T_z\)	[ h ]	Zone time or local time
\(T_j\)	[ h ]	Equation of time
\(K\)	[ ° ]	Local Constant
\(Cor_{DST}\)	[ h ]	Correction for daylight saving time

External conditions

External time series are needed to calculate the solar radiation on an inclined plane in energyPRO.

These time series include solar radiation. Optimally, the solar radiation is divided into beam radiation, Ib and diffuse radiation, Id. Alternately, the solar radiation comes as total radiation, I.

If the solar radiation comes as total radiation the diffuse and the beam radiation can be calculated as follows (Reindl, D.T, et al., ”Diffuse Fraction Correlations” Solar Energy, vol. 31, No 5, October 1990):

Interval: \(0 \leq K_T \leq 0.3\)	Constraint: \(I_d/I \leq 1.0\)	\(I_d/I = 1.020 - 0.254 ^* K_T + 0.0123 ^* sin α\)
Interval: \(0.3 < K_T < 0.78\)	Constraint: \(0.1 \leq I_d/I \leq 0.97\)	\(I_d/I = 1.400 - 1.749 ^* K_T + 0.0177 ^* sin α\)
Interval: \(0.78 \leq K_T\)	Constraint: \(0.1 \leq I_d/I\)	\(I_d/I = 0.486 ^* K_T + 0.0182 ^* sin α\)

Where \(K_T\) is the ratio of total radiation on a horizontal plane to extraterrestrial radiation: $$ K_T = \frac{I}{I_o} $$ Io is defined as: $$ I_o = I_{sc} * cosθ_z $$ Where \(I_{sc}\) is the solar constant, 1367 \(w/m^2\)

            \(\theta_z\) is the solar zenith angle, described in Methods, Solar, Radiation.

The beam radiation is $$ I_b = I - I_d $$

Radiation on solar collector or photovoltaic

This section describes the calculation of radiation on unshaded surface. Methods, Solar, Array contains the effects of array shading.

The time series with solar radiation are radiation on horizontal plane. Most often the solar collector or photovoltaic is inclined. Therefore the first task is to convert the radiation on horizontal to the inclined plane.

Beam radiation

The relation between the beam radiation on an inclined plane and the beam radiation on horizontal is giving by the factor \(R_b\). $$ R_b = \frac{cosθ}{cosθ_z} $$

where \(\theta\) is angle of incidence of beam radiation on inclined plane.

The solar zenith angle is specified by the formula: $$ cosθ_z = sinδ * sinΦ + cosδ * cosΦ * cosω $$

Where \(\delta\) is the solar declination angle

            \(\phi\) is the latitude

            \(\omega\) is the hour angle

The solar declination angle is approximately specified by: $$ \delta = 23.45 * sin\left(360 * \frac{284 + n}{365}\right) $$

Where \(n\) is the day of the year.

The hour angle, \(\omega\) is defined by:

\[ \omega = 1 5 \frac{d e g r e e s}{h o u r} * \left( T_{T S T} - 1 2 \right) \]

Where \(T_{TST}\) is True Solar Time. True Solar Time is defined in the section below.

The beam radiation on an inclined plane is found by the following formula:

\[ cosθ = sinδ * sinΦ * cos s - sinδ * cosΦ * sin s * cosλ\\ + cosδ * cosΦ * cos s * cosω\\ + cosδ * sinΦ * sin s * cosλ * cosω\\ + cosδ * sin s * sinλ * sinω \]

where \(s\) is the inclination of the plane

            \(\lambda\) is the plane’s orientation.

The beam radiation on an inclined plane:

\[ I_{dir} = I_b * R_b \]

True Solar Time

The converting from local time or Zone time to true solar time is done by:

\[ T_{T S T} = T_z + T_j + K - C o r_{D S T} \]

Where \(T_z\) is zone time or local time

            \(T_j\) is the equation of time

            \(K\) is the Local Constant

            \(Cor_{DST}\) is correction for daylight saving time

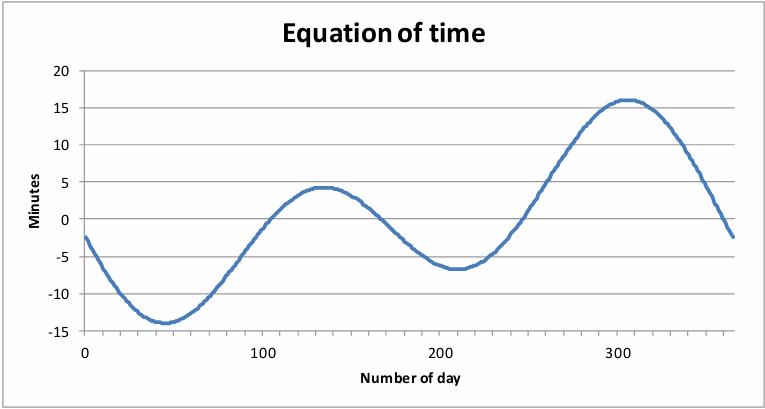
The equation of time, \(T_j\), is the deviation over the year between the local time and the true solar time. \(T_j\) is found by

\[ T_j = 2 2 9 . 2 * \left( 0 . 0 0 0 0 7 5 + 0 . 0 0 1 8 6 8 * \cos B - 0 . 0 3 0 2 7 7 * \sin B - 0 . 0 1 4 6 1 5 * \cos ( 2 B ) - 0 . 0 4 0 8 9 * \sin ( 2 B ) \right) \]

Where B is in degrees and found by

\[ B = \left( n - 1 \right) * \frac{360}{365} \]

Where \(n\) is number day in year.

\(T_j\) varies from approximately -15 minutes to approximately + 17 minutes.

The Local Constant, \(K\), is found by

\[ K = - 4 \frac{\min}{d e g r e e} * \left( l_{m} - l_{s t} \right) \ d e g r e e \]

Where \(l_m\) is the standard meridian for the local time zone and \(l_{st}\) is the longitude of the location in question.

The correction, \(Cor_{DST}\) for daylight saving time has the value 1 from start to end of Daylight-Saving Time and 0 in the standard time.

The true solar time shall be in the middle of each time step. If the sun rises or sets in the time step, the true solar time shall be in the middle from sunrise to end of time step when in the morning, and in the middle from start of time step and sunset, when in the evening.

Diffuse radiation

The ratio between the diffuse radiation on an inclined plane and horizontal is given by (Reindl, D.T., Beckman, W.A. and Duffie, J.A., “Evaluation of Hourly Tilted Surface Radiation Models”, Solar Energy, Vol. 45, No. 1, (1990), pp. 9-17):

\[ R_d=0.5*(1-A_I )*(1+cos⁡ s )*\left(1+(f)*sin^3({s   /   2}) \right)+A_I*R_b \]

Where \(A_I\) is Anisotropy index

             f is modulating factor

\(A_I\) is defined as follows:

\[ A_I= I_{bn}/I_{on} \]

Where \(I_{bn}\) is beam radiation at normal incidence

           \(I_{on}\) is extraterrestrial radiation at normal incidence

\(f\) is defined as follows:

\[ f= √(I_b/I) \]

The extraterrestrial radiation at normal incidence is set equal to the Solar Constant.

The beam radiation at normal incidence is found by setting \(\theta\) = 0.Hereby the diffuse radiation on the inclined plane:

\[ I_{diff} = I_d * R_d \]

Reflected radiation

The contribution from radiation reflected from the ground is defined as follows:

\[ R_r = 0.5 * (1-cos s) * \rho \]

Where \(\rho\) is the reflection factor

\(\rho\) depends on local conditions, a typical value is 0.2, equal to ground covered by grass.

Hereby the reflected radiation becomes:

\[ I_{ref} = I * R_r \]

Total radiation

The total radiation on the inclined surface is the sum of the beam, diffuse and reflected radiation:

\[ I_s = I_{dir}+I_{diff}+I_{ref} \]

Array shading

Without array shading the calculated radiation on an inclined surface is valid for single rows of surface. Often, large scale solar collector or photovoltaic systems will be mounted on the ground in rows. The radiation will be reduced on the subsequent rows.

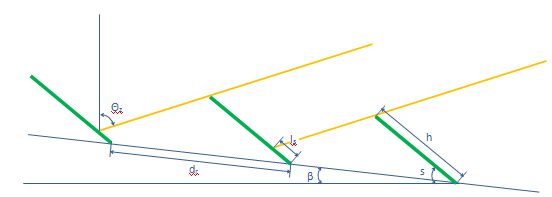
The reduction of the radiation depends on the following input data or solar data:

Variable	Unit	Description
\(β_{gr}\)	[ ° ]	The inclination of the ground
\(γ_{gr}\)	[ ° ]	The orientation of the ground related to south
s	[ ° ]	The inclination of the surfaces
\(γ_{surf}\)	[ ° ]	The orientation of the surfaces related to south
h	[ m ]	The height of surfaces
\(d_r\)	[ m ]	The distance between the rows related to the ground
\(\Phi\)	[ ° ]	The latitude of location
\(N_{rows}\)		The number of rows
\(\omega\)	[ ° ]	The solar hour angle
\(\theta_z\)	[ ° ]	The solar zenith angle

Beam radiation

If the inclination of the ground is zero, the surfaces of the solar collectors or PVs are orientated at south and the sun is in south, the length of the shadow can be calculated by the use of sinus relations:

\[ l_s = h - \frac{d_r}{sin(180-s-(90-\theta_z))} * sin(90-\theta_z) \]

However, the ground can have any inclination in any direction, the surfaces can have any inclination in any direction and the sun is deviating from south most of the day.

We need to find the length of the shadow on the surface in the hour angle plane, \(\omega\).

\[ l_{s\omega} = h_\omega - \frac{d_{r\omega}}{sin \left(180-s'_\omega - (90 - (\theta_z - \beta_{gr,\omega}))\right)} * sin(90-(\theta_z - \beta_{gr,\omega})) \]

Where \(l_{s\omega}\) is the length of the shadow on the surface

           \(h_\omega\) is the height of the surface

           \(d_{r\omega}\) is the distance between the rows

           \(s’_\omega\) is the surface’s inclination related to the ground

           \(\beta_{gr,\omega}\) is the inclination of the ground

           All in the hour angle plane, \(\omega\).

The height of the surface in the hour angle, \(h_\omega\) is found by the following cosine relation:

\[ h_\omega = \ \sqrt{{h_{g r \omega}}^{2} + \left( \sin s * h \right)^{2} - 2 * h_{g r \omega} * \left( \sin s * h \right) * \cos \left( 9 0 - \left( \beta_{g r , s u r f \omega} - \beta_{g r \omega} \right) \right)} \]

Where \(h_{gr\omega}\) is the height of the surface, when projected down on the ground:

\[ h_{g r \omega} = \ \frac{\cos s * h}{\cos \left( \beta_{g r , s u r f \omega} - \beta_{g r \omega} \right) * \cos \omega} \]

The inclination of the ground in the hour angle, \(\beta_{gr,\omega}\) is found by:

\[ \beta_{g r , \omega} = a s i n \left( \sin \beta_{g r} * \cos \left( \omega - \gamma_{g r} \right) \right) \]

The distance between the rows in the hour angle, \(d_{r\omega}\) is found by:

\[ d_{r \omega} = \ \frac{c o s \beta_{g r , s u r f}}{\cos {\left( \omega - \gamma_{s u r f} \right) * \cos \beta_{g r , \omega}}} * d_r \]

\(\beta_{gr,surf}\) is the grounds inclination in the orientation of the surfaces:

\[ \beta_{g r , s u r f} = a s i n \left( \sin \beta_{g r} * \cos \left( \gamma_{s u r f} - \gamma_{g r} \right) \right) \]

The surface’s inclination in the hour angle related to the inclination of the ground:

\[ {s '}_\omega = \arcsin \left( \frac{\sin {\left( 9 0 - \beta_{g r \omega} \right) * \sin s * h}}{h_\omega} \right) \]

The part of the total surface area in shadow, \(Sh_{frac}\) is calculated as follows:

\[ S h_{f r a c} = \ \frac{\left( N_{r o w s} - 1 \right) * m i n \left( \frac{l_s}{h_{\omega}} , 1 \right)}{N_{r o w s}} \]

Where Nrows is the number of rows.

With correction for array shading the beam radiation becomes:

\[ I_{d i r} = I_b * R_b * \left( 1 - S h_{f r a c} \right) \]

Diffuse radiation

The shadow impact on the diffuse radiation is visualized below:

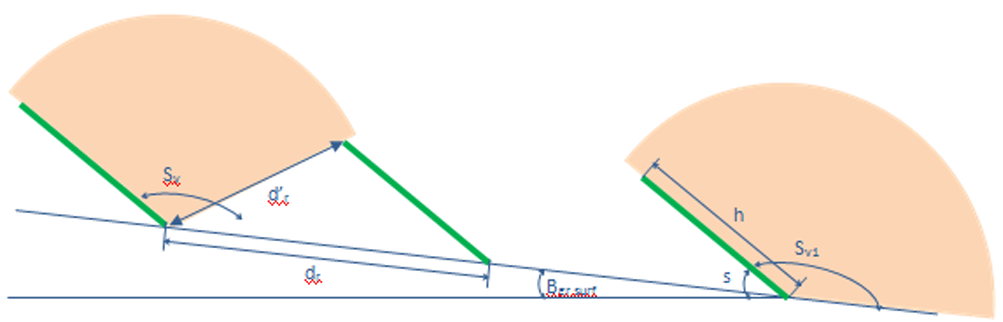
Where \(S_v\) is the angle of sky view of the rows affected by shading of proceeding row and \(S_{v1}\) is the sky view of the first row, which is not affected by shading, but where the inclination of the ground in the orientation of the surfaces is taking into consideration.

\(S_{v1}\) is equal to \(180 – (s – \beta_{gr, surf})\)

The ratio between the diffuse radiation on first row and horizontal, \(R_{d1}\) is given by:

\[ R_{d 1} = 0 , 5 * \left( 1 - A_I \right) * \left( 1 + \cos {( s - \beta_{g r , s u r f} )} \right) * \left( 1 + ( f ) * \sin^3 \left( \frac{s}{2} \right) \right) + A_I * R_b \]

The ratio between the diffuse radiation on subsequent rows and horizontal, \(R_d\) is given by:

\[ R_d = 0 , 5 * \left( 1 - A_I \right) * \left( 1 + \cos {( 1 8 0 - s_v )} \right) * \left( 1 + ( f ) * \sin^3 \left( \frac{s}{2} \right) \right) + A_I * R_b * ( 1 - S h_{f r a c} ) \]

The height of the collector is split in 10 pieces. The \(S_v\) and \(R_d\) is calculated at the middle for each of them and the average \(R_d\) is used.

\(S_v\) is found by the following cosine relation:

\[ S_v = \arccos \left( \frac{h^2 + {d '_r}^2 - {d_r}^2}{2 * h * {d '}_r} \right) \]

Where \(d’_r\) is the distance between the bottom of the row and the top of the preceding row.

\(d’_r\) is found by the following cosine relation:

\[ {d '}_r = \sqrt{h^2 + {d_r}^2 - 2 * h * d_r * \cos \left( s - \beta_{g r , s u r f} \right)} \]

The resulting \(R_{d,sh}\) becomes:

\[ R_{d , s h} = \frac{\left( \left( N_{r o w s} - 1 \right) * R_{d} + R_{d 1} \right)}{N_{r o w s}} \]

The diffuse radiation on the inclined surface when taking shading into consideration becomes:

\[ I_{d i f f} = \ I_d * R_{d , s h} \]

Reflected radiation

The reflected radiation ratio when taking shading into consideration is divided into the beam, \(R_{r,b}\) and diffuse, \(R_{r, d}\) radiation. Further, the ratio is different for the first, \({R_r1}\) and the following rows, \(R_{rn}\).

Beam and diffuse reflected radiation on the first rows are given as:

\[ R_{r 1 , b} = R_{r 1 , d} = 0 . 5 * \left( 1 - \cos {( s - \beta_{g r , s u r f} )} \right) * 0 . 2 \]

The reflected radiation on the proceeding rows is calculated as ratio of the reflected radiation on the first row, \(r_{p-1}\).

The beam reflected radiation on the proceeding rows depends on the length of the beam on the ground, \(I_{sun}\). The length is zero if the surface is partly in shade, meaning that no beam radiation reach the ground in front of the row.

If the length of the beam on the ground is equal to h, \(r_{p-1,b}\) is set to 1. The length is calculated as follows:

\[ I_{s u n} = d_{r \omega} - \frac{h_\omega}{\sin \left( 9 0 - \theta '_{z \omega} \right)} * \sin \left( 1 8 0 - s'_{\omega} - \left( 9 0 - \theta '_{z \omega} \right) \right) \]

And \(r_{p-1,b}\) becomes:

\[ r_{p - 1 , b} = \ \frac{l_{s u n}}{h} \]

\[ R_{r n , b} = R_{r 1 , b} * r_{p - 1 , b} \]

The reflected beam radiation, \(R_{r,b}\) becomes:

\[ R_{r , b} = \frac{\left( \left( N_{r o w s} - 1 \right) * R_{r n , b} + R_{r 1 , b} \right)}{N_{r o w s}} \]

The reflected diffuse radiation on the proceeding rows as ratio of the reflected diffuse radiation on the first row, \(r_{p-1,d}\) has been defined as follows:

\[ r_{p - 1 , d} = \ \frac{S_v}{\left( 1 8 0 - ( s - \beta_{g r , s u r f} ) \right)} \]

The diffuse reflected radiation, \(R_{rn,d}\) becomes:

\[ R_{r n , d} = R_{r 1 , d} * r_{p - 1 , d} \]

The overall reflected diffuse radiation, \(R_{r,d}\) becomes:

\[ R_{r , d} = \frac{\left( \left( N_{r o w s} - 1 \right) * R_{r n , d} + R_{r 1 , d} \right)}{N_{r o w s}} \]

The reflected radiation on the inclined surface when taking shading into consideration becomes:

\[ I_{r e f} = \ I_b * R_{r , b} + I_d * R_{r , d} \]

Solar Collector

The formula for a solar collector is as follows (without Incidence angle modifier):

\[ Y = A * \left(I_s * n_o - a_l * (t_m - t_a) - a_2 * (t_m - t_a) ^2 \right) \]

where Y is Heat production, [\(W\)].

           \(A\) is solar collector area, [\(m^2\)]

           \(I_s\) is solar radiation on solar collector, [\(W/m^2\)]

           \(t_m\) is collectors average temperature, [ °C],
                an average between the temperature of the cold water entering the collector and the hot water leaving the collector

           \(t_a\) is ambient temperature, [ °C]. For the best results the ambient temperatures should be hourly.

The efficiency of the solar collector is defined by three parameters:

           \(n_o\): Intercept (maximum) of the collector efficiency, [-]

           \(a_1\): The first-order coefficient in collector efficiency equation, [\(W/(m^2 °C\))]

           \(a_2\): The second-order coefficient in collector efficiency equation, [\(W/(m^2 °C)^2\)]

These 3 parameters are available for collectors tested according to ASHRAE standards and rated by SRCC (ASHRAE, 2003; SRCC,1995), as well as for collectors tested according to the recent European Standards on solar collectors (CEN, 2001). Many examples of collector parameters can be found on the internet (e.g. SPF, 2004).

Note: It is important to make sure that collector area entered as a parameter match the area used when determining the values of \(n_o\), \(a_1\) and \(a_2\). Typically, efficiency curves are provided for gross area in the US and aperture area in Europe.

Furthermore, the model includes Incidence Angle Modifier, IAM or \(K_\theta\). The sun is not always located perpendicular to the collector plane; the incidence angle generally changes both during the course of a day and throughout the year. The transmittance of the cover glazing for the collector changes with the incidence angle.

Incidence angle modifier, Flat plate solar collector

Typically, the Incidence angle modifier for a flat plate solar collector looks as below:

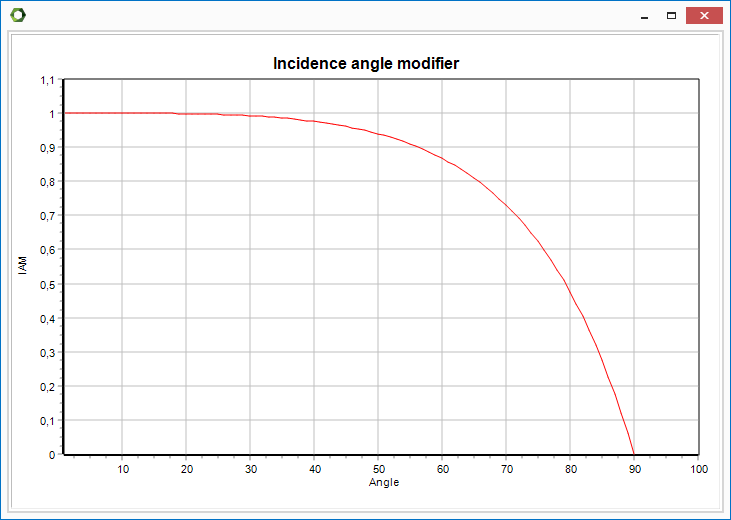
It can also be defined as follow:

\[ K_\theta = 1-tan^a(\theta/2) \]

where \(\theta\) is the incidence angle on the collector.

           \(a\) is the measured coefficient.

Including \(K_\theta\) the formula for the heat production from the solar collector becomes:

\[ Y = A * \left((I_{beam} * K_\theta + (I_{diffuse}) * K_{60°}) * N_0 - a_1 * (t_m - t_a) - a_2 * (t_m - t_a) ^2 \right) \]

The radiation is split into beam radiation and diffuse radiation. Since the diffuse radiation per definition has no incidence angle the IAM at 60° is used.

Incidence angle modifier, Evacuated tube solar collector

Evacuated tube collectors are optically non-symmetric.

The longitudinal incidence angle is measured in a plane that is perpendicular to the collector plane and contains the collector azimuth. The corresponding IAM is referred to as the longitudinal IAM, or altitude modifier.

The transversal incidence angle is measured I a plane that is perpendicular to both the collector aperture and the longitudinal plane. The corresponding IAM is referred to as the transversal IAM, or azimuthal modifier.

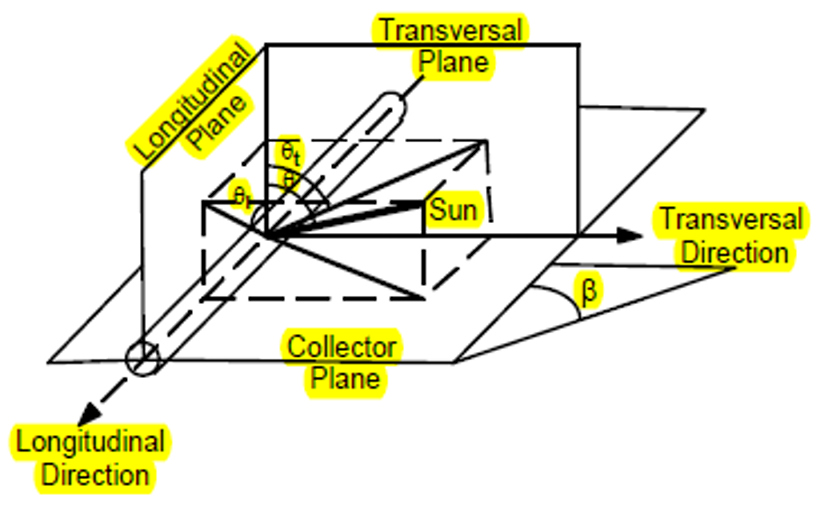
The Longitudinal incidence angle, \(\theta_l\) is found by:

\[ \theta_{l} = a b s \left( a t a n \left( \tan \theta_{Z} * \cos ( \omega - \gamma ) \right) - s \right) \]

where \(\theta_Z\) is the Solar zenith angle

           \(\omega\) is the hour angle

           \(\lambda\) is the orientation of the solar collector

           \(s\) is the inclination of the solar collector

And transversal incidence angle, \(\theta_t\) is found by:

\[ \theta_t = a b s \left( a t a n \left( \frac{\sin \theta_Z * \sin ( \omega - \gamma )}{\cos \theta} \right) \right) \]

where \(\theta\) is the angle of incidence of beam radiation on inclined plane.

When specifying the evacuated tube solar collector, the IAM is specified for both the longitudinal and the transversal incidence angle.

The overall Incidence Angle Modifier for beam radiation, \(K_\theta(\theta_l,\theta_t)\) is found by:

\[ K_\theta \left( \theta_l , \theta_t \right) = K_\theta \left( \theta_l \right) * K_\theta \left( \theta_t \right) \]

The values of \(K_\theta(\theta_l)\) and \(K_\theta(\theta_t)\) is found by interpolating between the nearest values in the table of Incidence angle modifier.

The IAM for diffuse radiation is calculated by evaluating the ratio of absorbed diffuse radiation over to incident diffuse radiation over the sky dome for a horizontal collector, assuming isotropic diffuse radiation:

\[ K_{\theta d i f f} = \frac{4}{\pi} \int_{2}^{\frac{\pi}{2}} {\int_{2}^{\frac{\pi}{2}} {K_\theta ( \theta , \omega ) * \cos \theta * \sin \theta * d \theta * d \omega}} \]

This integration is performed once at the start of the simulation, with the user supplied IAM data.

Including \(K_\theta\) the formula for the heat production from the solar collector becomes:

\[ Y = A * \left((I_{beam} * K_\theta + (I_{diffuse}) * K_{\theta diff}) * N_0 - a_1 * (t_m - t_a) - a_2 * (t_m - t_a)^2 \right) \]

Photovoltaic

The electricity production from a Photovoltaic module, \(P_{pv}\), can be expressed as follows:

\[ P_{pv} = P_{Max} * \frac{I_s}{I_{STC}} * [1 - \gamma_s * (T_{cell} - T_{STC})] \]

where \(P_{max}\) is installed capacity [\(W\)]

           \(I_s\) is solar radiation [\(W/m^2\)]

           \(I_{STC}\) is radiation at standard conditions (\(1000 W/m^2\)) [\(W/m^2\)]

           \(\gamma_s\) is temperature coefficient for module efficiency [-]

           \(T_{cell}\) is operation cell temperature [\(°C\)]

           \(T_{STC}\) is the cell temperature at standard conditions (\(25 °C\)) [\(°C\)]

The operation cell temperature is calculated by the following formula (Antonio Luque and Steven Hegedus (2003)):

\[ T_{cell} = T_{at} + I_s * \left(\frac{NOCT - 20°C}{800W/m^2}\right) \]

where \(T_{at}\) is ambient temperature

           NOCT is Nominal Operating Cell Temperature

Hereto come losses from the pv-module to the grid, \(\gamma_{misc}\), such as miscellaneous PV array losses and other power conditioning losses.

The power production at grid becomes:

\[ P_{elec} = P_{pv} * (1 - \lambda_{misc}) \]